Análise detallada do circuíto da serie RC
2024-05-08
20572
O circuíto da serie RC, composto por un resistor e un condensador, serve como compoñente fundamental tanto nos deseños de sistemas electrónicos básicos como avanzados.Axuda a comprender os principios clave como a resposta de frecuencia, o cambio de fase e o filtrado de sinal, que xogan un papel significativo no deseño de circuítos e o procesamento de sinal.Esta exploración abrangue os conceptos básicos teóricos e esténdese a aplicacións prácticas a través de experimentos e simulacións.Ao montar físicamente o circuíto ou modelalo dixitalmente, os estudantes poden comprender visualmente o proceso de carga e os efectos dos ións do compoñente V ariat, facendo que os conceptos complexos sexan máis accesibles e memorables.
Catálogo

Figura 1: diferentes tensións de saída dos circuítos RC
Introdución ao circuíto RC
Un circuíto RC, curto para o circuíto de resistencia-capacitancia, é fundamental na electrónica para manipular sinais a través de resistencias e condensadores.Estes circuítos son especialmente coñecidos pola súa capacidade para cambiar fases e sinais de filtro, empregando arranxos sinxelos destes compoñentes.Un circuíto RC básico, a miúdo chamado circuíto RC de primeira orde, normalmente inclúe só un resistor e un condensador.
Nunha configuración típica, a tensión de entrada aplícase á disposición en serie dun resistor e un condensador.A saída pódese extraer a través do resistor ou do condensador, cada un dando respostas diferentes ás frecuencias de sinal debido ás características únicas do condensador.Esta versatilidade permite que os circuítos RC realicen unha variedade de roles en dispositivos electrónicos, como sinais de acoplamiento e filtrado ou incluso convertendo as formas de onda cando se someten a unha tensión de paso.
O circuíto RC pódese configurar de varias maneiras: series, paralelas ou unha combinación de ambos, coñecidos como series-paralelas.Cada configuración afecta ás frecuencias do sinal de forma diferente: as conexións en serie tenden a atenuar frecuencias baixas, mentres que as conexións paralelas úsanse para amortecer frecuencias máis altas.Esta diferenza débese principalmente á forma en que as resistencias e condensadores interactúan co circuíto;As resistencias se opoñen directamente á corrente mentres os condensadores almacenan e liberan, impactando como o circuíto responde a diferentes frecuencias.
A diferenza dos circuítos que inclúen indutores, como os circuítos LC, os circuítos RC sinxelos non poden resoar xa que as resistencias non almacenan enerxía.Este atributo inflúe de xeito distinto como se utilizan os circuítos RC, centrándose na súa capacidade de filtrado en vez de almacenamento de enerxía ou resonancia.Cada configuración serve para un propósito específico, facendo que os circuítos RC sexan ferramentas versátiles tanto no estudo teórico como na aplicación práctica no deseño electrónico.
Circuíto da serie RC
Un circuíto da serie RC, esencialmente composto por un resistor (R) e un condensador (C) en serie, opera cun principio sinxelo.Cando o interruptor do circuíto está pechado, o condensador comeza a cargarse da tensión aplicada (V), iniciar un fluxo de corrente a través do circuíto.A medida que o condensador cobra, a corrente aumenta gradualmente ata que o condensador alcance a súa capacidade, momento no que deixa de aceptar a carga e a corrente estabilízase no seu valor máximo, calculado como 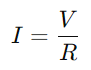 .
.
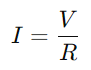 .
.O proceso de carga do condensador pódese describir matematicamente pola ecuación 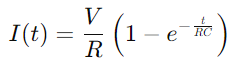 , onde eu é o actual, V é a tensión, R é a resistencia, C é a capacitancia, t é o tempo, e e é a base do logaritmo natural.Esta fórmula reflicte como a corrente cambia co paso do tempo a medida que o condensador cobra, co produto dos valores de resistencia e capacitancia (RC) que definen a constante de tempo do circuíto, indicativo da velocidade coa que o condensador cobra.
, onde eu é o actual, V é a tensión, R é a resistencia, C é a capacitancia, t é o tempo, e e é a base do logaritmo natural.Esta fórmula reflicte como a corrente cambia co paso do tempo a medida que o condensador cobra, co produto dos valores de resistencia e capacitancia (RC) que definen a constante de tempo do circuíto, indicativo da velocidade coa que o condensador cobra.
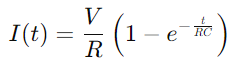 , onde eu é o actual, V é a tensión, R é a resistencia, C é a capacitancia, t é o tempo, e e é a base do logaritmo natural.Esta fórmula reflicte como a corrente cambia co paso do tempo a medida que o condensador cobra, co produto dos valores de resistencia e capacitancia (RC) que definen a constante de tempo do circuíto, indicativo da velocidade coa que o condensador cobra.
, onde eu é o actual, V é a tensión, R é a resistencia, C é a capacitancia, t é o tempo, e e é a base do logaritmo natural.Esta fórmula reflicte como a corrente cambia co paso do tempo a medida que o condensador cobra, co produto dos valores de resistencia e capacitancia (RC) que definen a constante de tempo do circuíto, indicativo da velocidade coa que o condensador cobra.
Figura 2: circuíto da serie RC
A descarga prodúcese cando se abre o interruptor, revertendo o proceso: a enerxía almacenada no condensador é liberada, facendo que a corrente flúa no sentido contrario ata que o condensador se drena.Este ciclo de carga e descarga é crucial en aplicacións como a conversión do sinal, o filtrado e os circuítos de cronometraxe debido á forma previsible en que o cambio de corrente e tensión.

Figura 3: curtocircuíto da serie RC
O comportamento do circuíto da serie RC tamén varía coa frecuencia.En frecuencias baixas, o condensador actúa máis como un circuíto aberto, impedindo moito o fluxo de corrente.A medida que a frecuencia aumenta, a reactancia capacitiva diminúe, facilitando a transmisión da corrente.Este cambio de impedancia coa frecuencia permite que o circuíto da serie RC actúe como un filtro, atenuando de forma selectiva as frecuencias por baixo dun certo limiar (frecuencia de xiro 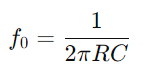 ).
).
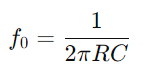 ).
).
Figura 4: Carga e descarga de circuítos da serie RC
Ademais das operacións en estado estacionario, os circuítos RC tamén se estudan para as súas respostas transitorias cando se somete a cambios súbitos de tensión, como cando se acende ou desactive unha fonte de alimentación DC.Este escenario denomínase un proceso transitorio, onde o circuíto transita dun estado estable a outro.A dinámica deste proceso depende significativamente da constante de tempo de RC, que rexe o rápido que o circuíto reacciona aos cambios.
En última instancia, os circuítos da serie RC serven múltiples funcións tanto en aplicacións de corrente continua como de CA, manexando tarefas que van desde atrasar sinais ata integrar ou acoplar varios elementos de circuíto.Esta versatilidade deriva das interaccións únicas entre o resistor e o condensador, que xuntos determinan a resposta global do circuíto a cambios de tensión e frecuencia.

Figura 5: diagrama de circuítos de serie RC e fórmula de frecuencia
Nun circuíto da serie RC, a interacción entre a resistencia (R) e o condensador (C) inflúe tanto no fluxo de corrente como na distribución de tensión.O papel principal do resistor é regular o fluxo actual.Esta relación é cuantificada pola lei de Ohm, que afirma 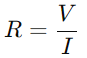 , onde V é tensión e I é actual.Esencialmente, a resistencia actúa como pescozo de botella, controlando a cantidade de electricidade que pode pasar nun momento dado.
, onde V é tensión e I é actual.Esencialmente, a resistencia actúa como pescozo de botella, controlando a cantidade de electricidade que pode pasar nun momento dado.
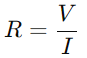 , onde V é tensión e I é actual.Esencialmente, a resistencia actúa como pescozo de botella, controlando a cantidade de electricidade que pode pasar nun momento dado.
, onde V é tensión e I é actual.Esencialmente, a resistencia actúa como pescozo de botella, controlando a cantidade de electricidade que pode pasar nun momento dado.A función do condensador é lixeiramente máis complexa, xa que almacena temporalmente a enerxía eléctrica e logo a libera no circuíto.A tensión a través do condensador (VC) correlaciona coa súa carga almacenada (P) e calcúlase usando a fórmula  .Esta relación pon de manifesto a capacidade do condensador para manter a carga, afectando directamente á tensión que exhibe.Durante a operación, a dinámica de carga e descarga do condensador é vital para comprender os circuítos RC.A constante de tempo (τ), definido como
.Esta relación pon de manifesto a capacidade do condensador para manter a carga, afectando directamente á tensión que exhibe.Durante a operación, a dinámica de carga e descarga do condensador é vital para comprender os circuítos RC.A constante de tempo (τ), definido como 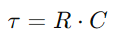 , mide a rapidez con que o condensador alcanza aproximadamente o 63,2% da tensión completa subministrada pola fonte (V0).Esta constante de tempo é indicativa de como o circuíto se adapta aos cambios de entrada, coa resistencia e as propiedades do condensador que dictan o ritmo destes axustes.
, mide a rapidez con que o condensador alcanza aproximadamente o 63,2% da tensión completa subministrada pola fonte (V0).Esta constante de tempo é indicativa de como o circuíto se adapta aos cambios de entrada, coa resistencia e as propiedades do condensador que dictan o ritmo destes axustes.
 .Esta relación pon de manifesto a capacidade do condensador para manter a carga, afectando directamente á tensión que exhibe.Durante a operación, a dinámica de carga e descarga do condensador é vital para comprender os circuítos RC.A constante de tempo (τ), definido como
.Esta relación pon de manifesto a capacidade do condensador para manter a carga, afectando directamente á tensión que exhibe.Durante a operación, a dinámica de carga e descarga do condensador é vital para comprender os circuítos RC.A constante de tempo (τ), definido como 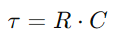 , mide a rapidez con que o condensador alcanza aproximadamente o 63,2% da tensión completa subministrada pola fonte (V0).Esta constante de tempo é indicativa de como o circuíto se adapta aos cambios de entrada, coa resistencia e as propiedades do condensador que dictan o ritmo destes axustes.
, mide a rapidez con que o condensador alcanza aproximadamente o 63,2% da tensión completa subministrada pola fonte (V0).Esta constante de tempo é indicativa de como o circuíto se adapta aos cambios de entrada, coa resistencia e as propiedades do condensador que dictan o ritmo destes axustes.A tensión a través do condensador nun momento dado durante a carga vén dado por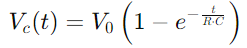 , ilustrando un aumento non lineal a medida que o condensador enche.Esta ecuación describe como a taxa de carga diminúe a medida que o condensador se achega a plena capacidade.
, ilustrando un aumento non lineal a medida que o condensador enche.Esta ecuación describe como a taxa de carga diminúe a medida que o condensador se achega a plena capacidade.
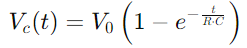 , ilustrando un aumento non lineal a medida que o condensador enche.Esta ecuación describe como a taxa de carga diminúe a medida que o condensador se achega a plena capacidade.
, ilustrando un aumento non lineal a medida que o condensador enche.Esta ecuación describe como a taxa de carga diminúe a medida que o condensador se achega a plena capacidade.Pola contra, durante a descarga, a tensión do condensador diminúe segundo 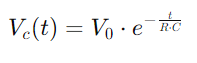 , retratando unha diminución lineal da enerxía almacenada co paso do tempo.Este proceso proporciona unha imaxe clara de como a enerxía se libera do condensador de volta ao circuíto.En aplicacións de CA, a diferenza de fase entre a tensión e a corrente, φ, faise crítico.Esta diferenza, calculada como
, retratando unha diminución lineal da enerxía almacenada co paso do tempo.Este proceso proporciona unha imaxe clara de como a enerxía se libera do condensador de volta ao circuíto.En aplicacións de CA, a diferenza de fase entre a tensión e a corrente, φ, faise crítico.Esta diferenza, calculada como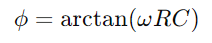 onde Ω Representa a frecuencia angular, mostra o atraso causado polo condensador, que afecta o tempo entre os fluxos de corrente e os cambios de tensión nos compoñentes.
onde Ω Representa a frecuencia angular, mostra o atraso causado polo condensador, que afecta o tempo entre os fluxos de corrente e os cambios de tensión nos compoñentes.
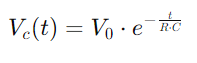 , retratando unha diminución lineal da enerxía almacenada co paso do tempo.Este proceso proporciona unha imaxe clara de como a enerxía se libera do condensador de volta ao circuíto.En aplicacións de CA, a diferenza de fase entre a tensión e a corrente, φ, faise crítico.Esta diferenza, calculada como
, retratando unha diminución lineal da enerxía almacenada co paso do tempo.Este proceso proporciona unha imaxe clara de como a enerxía se libera do condensador de volta ao circuíto.En aplicacións de CA, a diferenza de fase entre a tensión e a corrente, φ, faise crítico.Esta diferenza, calculada como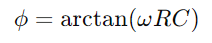 onde Ω Representa a frecuencia angular, mostra o atraso causado polo condensador, que afecta o tempo entre os fluxos de corrente e os cambios de tensión nos compoñentes.
onde Ω Representa a frecuencia angular, mostra o atraso causado polo condensador, que afecta o tempo entre os fluxos de corrente e os cambios de tensión nos compoñentes.En xeral, a resistencia limita e dirixe o fluxo de corrente mentres o condensador almacena e modula a tensión.Xuntos, determinan as características de resposta do circuíto, como a rapidez que pode cargar e descargar e os cambios de fase que se producen en escenarios de corrente alterna.Este comportamento combinado sustenta as operacións fundamentais dos circuítos da serie RC, tornándoos integrais en diversas aplicacións electrónicas.
Ecuacións básicas do circuíto da serie RC
Para comprender o comportamento dun circuíto da serie RC, é crucial comezar coas ecuacións básicas que describen a súa resposta aos cambios na tensión de entrada.Supoña que temos unha tensión de entrada cambiante representada como Vin (T), coa tensión a través da resistencia etiquetada como VR (T) e a través do condensador como VC (T).Nun circuíto de serie, a mesma corrente, I (t) flúe a través do resistor e do condensador.
Aplicando a lei de tensión de Kirchhoff (KVL), que afirma que a tensión total arredor de calquera bucle pechado nun circuíto debe igualar cero, descubrimos que a tensión de entrada é igual á suma das tensións a través da resistencia e do condensador:

A tensión a través da resistencia pódese calcular mediante a lei de Ohm:
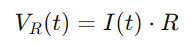
Para o condensador, a tensión VC (T) está relacionada coa carga Q (T) que mantén, dada por:
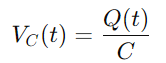
Dado que a corrente defínese como a taxa de fluxo de carga, temos:
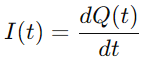
Por substituír Q (T) na ecuación para VC (T)e usando o derivado de carga I (t), Derivamos a ecuación diferencial principal para o circuíto da serie RC:

Substituíndo máis Q (T) coa integral de I (t), conseguimos:
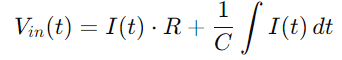
Para a corrente i (t), tendo en conta a taxa de cambio de tensión entre o condensador, empregamos:
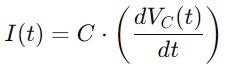
A integración de todas estas relacións ofrécenos a ecuación diferencial que describe a tensión a través do condensador:
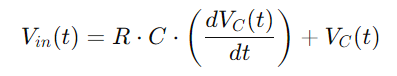
Esta é unha ecuación diferencial lineal de primeira orde que capta o cambio de tensión dependente do tempo a través do condensador.Resolver esta ecuación permítenos describir con precisión como evoluciona a tensión do condensador.Esta comprensión é fundamental para analizar os ciclos de carga e descarga do condensador, así como a resposta do circuíto a diferentes frecuencias.Este enfoque completo ofrece unha visión profunda das características dinámicas do circuíto da serie RC.

Figura 6: ecuación diferencial de tensión
Impedancia do circuíto da serie RC
Para reescribir a descrición dun circuíto da serie RC, con foco na interacción humana e unha explicación directa e simplificada, imos mellorar as experiencias tanxibles e as operacións paso a paso implicadas mantendo a mensaxe e a coherencia básica:
Nun circuíto da serie RC, o resistor e o condensador funcionan en tándem para controlar o fluxo de electricidade, crucial ao tratar as correntes alternas.A impedancia total do circuíto, representada como 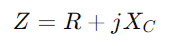 , combina a resistencia R e a reactancia capacitiva XC.A característica clave desta configuración é que os valores de impedancia para ambos os compoñentes varían cos cambios de frecuencia.A medida que aumenta a frecuencia, a impedancia do condensador diminúe, permitindo pasar máis corrente, mentres que a resistencia permanece esencialmente constante.
, combina a resistencia R e a reactancia capacitiva XC.A característica clave desta configuración é que os valores de impedancia para ambos os compoñentes varían cos cambios de frecuencia.A medida que aumenta a frecuencia, a impedancia do condensador diminúe, permitindo pasar máis corrente, mentres que a resistencia permanece esencialmente constante.
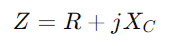 , combina a resistencia R e a reactancia capacitiva XC.A característica clave desta configuración é que os valores de impedancia para ambos os compoñentes varían cos cambios de frecuencia.A medida que aumenta a frecuencia, a impedancia do condensador diminúe, permitindo pasar máis corrente, mentres que a resistencia permanece esencialmente constante.
, combina a resistencia R e a reactancia capacitiva XC.A característica clave desta configuración é que os valores de impedancia para ambos os compoñentes varían cos cambios de frecuencia.A medida que aumenta a frecuencia, a impedancia do condensador diminúe, permitindo pasar máis corrente, mentres que a resistencia permanece esencialmente constante.A impedancia, denotada como Z e medido en OHMS (Ω), xoga un papel crítico na determinación de como reacciona o circuíto á corrente alterna.Como nos circuítos da serie RL, a resistencia R e reactancia capacitiva xC dun circuíto RC forma un triángulo coñecido como o triángulo de impedancia.Este triángulo está relacionado estreitamente co triángulo de tensión e aplicando o teorema pitagórico, pode calcular a impedancia total do circuíto.

Figura 7: fórmula de cálculo do circuíto de serie RC
Cando se trata de aplicacións prácticas, considere auriculares, que usan estes principios.Os auriculares de alta impedancia, a miúdo superiores a 200 ohms, úsanse normalmente con ordenadores de escritorio, amplificadores de potencia e equipos de audio profesionais.Estes modelos de alta impedancia coinciden ben coas capacidades de saída da electrónica de calidade profesional.Ao usar estes auriculares, é crucial axustar o volume gradualmente para evitar a sobrecarga e danar os delicados compoñentes internos, como a bobina de voz.
Pola contra, os auriculares de baixa impedancia, normalmente por baixo dos 50 ohmios, son preferidos para dispositivos portátiles como reprodutores de CD, reprodutores de MD ou reprodutores MP3.Estes auriculares requiren menos enerxía para ofrecer audio de alta calidade, tornándoos ideais para uso móbil.Non obstante, tamén precisan unha atención minuciosa aos niveis de sensibilidade para garantir un rendemento óptimo e evitar danos nos auriculares ou audición.

Figura 8: Diagrama de impedancia do circuíto da serie RC
Procedementos de admisión e análise dos circuítos da serie RC
A admisión mide a facilidade un circuíto da serie RC pode realizar electricidade, calculada como a inversa de impedancia ( ).Este valor integra tanto a resistencia (R) e a reactancia (X) do circuíto.A resistencia oponse ao fluxo de corrente convertendo a enerxía eléctrica á calor, mentres que a reactancia almacena a enerxía temporalmente no circuíto.
).Este valor integra tanto a resistencia (R) e a reactancia (X) do circuíto.A resistencia oponse ao fluxo de corrente convertendo a enerxía eléctrica á calor, mentres que a reactancia almacena a enerxía temporalmente no circuíto.
 ).Este valor integra tanto a resistencia (R) e a reactancia (X) do circuíto.A resistencia oponse ao fluxo de corrente convertendo a enerxía eléctrica á calor, mentres que a reactancia almacena a enerxía temporalmente no circuíto.
).Este valor integra tanto a resistencia (R) e a reactancia (X) do circuíto.A resistencia oponse ao fluxo de corrente convertendo a enerxía eléctrica á calor, mentres que a reactancia almacena a enerxía temporalmente no circuíto.Para calcular a admisión
Comeza escribindo a impedancia 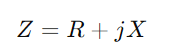 , onde R significa resistencia, X por reactancia e J. é a unidade imaxinaria.Use a fórmula y = 1/(R + jx).Esta operación implica números complexos e dános
, onde R significa resistencia, X por reactancia e J. é a unidade imaxinaria.Use a fórmula y = 1/(R + jx).Esta operación implica números complexos e dános 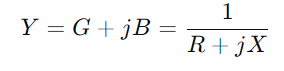 .Aquí, G é a condutancia (capacidade de fluxo actual) e B é a susceptencia (a capacidade do circuíto de reaccionar aos cambios na corrente).
.Aquí, G é a condutancia (capacidade de fluxo actual) e B é a susceptencia (a capacidade do circuíto de reaccionar aos cambios na corrente).
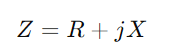 , onde R significa resistencia, X por reactancia e J. é a unidade imaxinaria.Use a fórmula y = 1/(R + jx).Esta operación implica números complexos e dános
, onde R significa resistencia, X por reactancia e J. é a unidade imaxinaria.Use a fórmula y = 1/(R + jx).Esta operación implica números complexos e dános 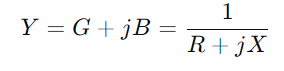 .Aquí, G é a condutancia (capacidade de fluxo actual) e B é a susceptencia (a capacidade do circuíto de reaccionar aos cambios na corrente).
.Aquí, G é a condutancia (capacidade de fluxo actual) e B é a susceptencia (a capacidade do circuíto de reaccionar aos cambios na corrente).
Figura 9: Calculadora de impedancia do circuíto RC en serie
Este cálculo revela non só a condutividade do circuíto, senón tamén as súas características de resposta dinámica, cruciais para a análise do circuíto de CA.A condutancia e a susceptancia, xuntadas, indican como o circuíto pasa a corrente e como almacena e libera enerxía.

Figura 10: fórmula de ángulo de fase
Aplicación práctica
Os enxeñeiros usan valores de admisión para mellorar o deseño de circuítos, especialmente en aplicacións de alta frecuencia como circuítos de frecuencia de radio.A axuste da admisión axuda á correspondencia de impedancias, á redución da reflexión do sinal e ao aumento da eficiencia da transmisión.
Ao estudar a resposta de admisión, os enxeñeiros poden avaliar e predicir o rendemento do circuíto en diversas condicións como a resposta de frecuencia, a estabilidade e a sensibilidade.Equipa cun osciloscopio e un xerador de sinal para medir a tensión e a corrente do circuíto en diferentes frecuencias.Concéntrase especialmente na frecuencia de corte para probar as predicións teóricas e validalas con observacións prácticas.Para circuítos de CA, comeza por determinar a reactancia (XC) do condensador con 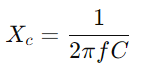 , onde f é a frecuencia do sinal.Calcula a impedancia total
, onde f é a frecuencia do sinal.Calcula a impedancia total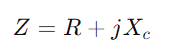 e logo admisión
e logo admisión  .
.
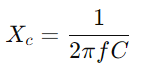 , onde f é a frecuencia do sinal.Calcula a impedancia total
, onde f é a frecuencia do sinal.Calcula a impedancia total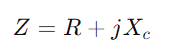 e logo admisión
e logo admisión  .
.Analizar a diferenza de fase usando 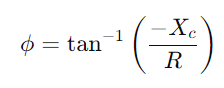 Para comprender a alteración da forma do sinal.Examine como o circuíto manexa diferentes frecuencias, especialmente nota o comportamento na frecuencia de corte
Para comprender a alteración da forma do sinal.Examine como o circuíto manexa diferentes frecuencias, especialmente nota o comportamento na frecuencia de corte 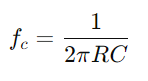 , onde o circuíto pasa de pasar a sinais de bloqueo.A avaliación de como a impedancia e a diferenza de fase varían coa frecuencia, é crucial para deseñar filtros eficaces e procesadores de sinal.Comenta como a selectividade de frecuencia, os cambios de fase e a atenuación do sinal debido ás propiedades do circuíto afectan a aplicacións prácticas como o filtrado e a afinación electrónica.
, onde o circuíto pasa de pasar a sinais de bloqueo.A avaliación de como a impedancia e a diferenza de fase varían coa frecuencia, é crucial para deseñar filtros eficaces e procesadores de sinal.Comenta como a selectividade de frecuencia, os cambios de fase e a atenuación do sinal debido ás propiedades do circuíto afectan a aplicacións prácticas como o filtrado e a afinación electrónica.
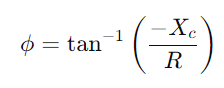 Para comprender a alteración da forma do sinal.Examine como o circuíto manexa diferentes frecuencias, especialmente nota o comportamento na frecuencia de corte
Para comprender a alteración da forma do sinal.Examine como o circuíto manexa diferentes frecuencias, especialmente nota o comportamento na frecuencia de corte 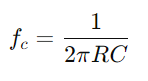 , onde o circuíto pasa de pasar a sinais de bloqueo.A avaliación de como a impedancia e a diferenza de fase varían coa frecuencia, é crucial para deseñar filtros eficaces e procesadores de sinal.Comenta como a selectividade de frecuencia, os cambios de fase e a atenuación do sinal debido ás propiedades do circuíto afectan a aplicacións prácticas como o filtrado e a afinación electrónica.
, onde o circuíto pasa de pasar a sinais de bloqueo.A avaliación de como a impedancia e a diferenza de fase varían coa frecuencia, é crucial para deseñar filtros eficaces e procesadores de sinal.Comenta como a selectividade de frecuencia, os cambios de fase e a atenuación do sinal debido ás propiedades do circuíto afectan a aplicacións prácticas como o filtrado e a afinación electrónica.Este enfoque descompón os procesos operativos en pasos manexables, enriquecendo a comprensión do usuario con ideas prácticas sobre o manexo e a análise dos circuítos da serie RC.

Figura 11: Características dos circuítos da serie RC
Diagrama de fases do circuíto da serie RC
Nun circuíto da serie RC, todos os elementos comparten a mesma corrente debido á súa configuración en serie.Esta corrente uniforme actúa como base para o noso diagrama de fases, o que axuda a visualizar a relación entre diferentes tensións e correntes no circuíto.Designemos esta corrente I Como fases de referencia, situado a cero graos no diagrama.No diagrama, a corrente I establécese horizontalmente á dereita, establecendo a liña de referencia de grao cero.A tensión a través da resistencia (UR) está en fase coa corrente porque as resistencias non causan ningún cambio de fase.Así, UR debúxase como un vector horizontal na mesma dirección que I, estendéndose desde a orixe.

Figura 12: diagrama de fases do circuíto da serie RC
En contraste, a tensión a través do condensador (UC) lidera a corrente en 90 graos debido á propiedade capacitiva de atrasar a fase actual.Esta tensión está representada por un vector vertical que apunta cara arriba, a partir da punta do UR vector.A tensión total U no circuíto está a suma vectorial de U Rand UC.Esta suma forma un triángulo dereito con UR e UC como lados adxacentes e opostos, respectivamente.A hipotenusa deste triángulo, estendéndose desde a orixe ata a punta do UC vector, representa U.
A corrente sinusoidal a través do circuíto vén dada polo pecado (ωt), onde IM é a máxima amplitude de corrente e Ω é a frecuencia angular.Consecuentemente, a tensión a través da resistencia é 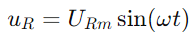 , reflectindo a forma de onda actual.A tensión a través do condensador é dada por
, reflectindo a forma de onda actual.A tensión a través do condensador é dada por 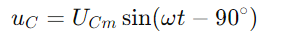 , indicando un cambio de fase de -90 ° (ou 90 graos por diante da corrente).O triángulo dereito do diagrama de fases aclara iso
, indicando un cambio de fase de -90 ° (ou 90 graos por diante da corrente).O triángulo dereito do diagrama de fases aclara iso non só está en magnitude senón tamén en relación en fase, co vector de tensión terminal (U) Completando o triángulo.
non só está en magnitude senón tamén en relación en fase, co vector de tensión terminal (U) Completando o triángulo.
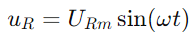 , reflectindo a forma de onda actual.A tensión a través do condensador é dada por
, reflectindo a forma de onda actual.A tensión a través do condensador é dada por 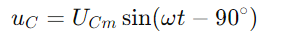 , indicando un cambio de fase de -90 ° (ou 90 graos por diante da corrente).O triángulo dereito do diagrama de fases aclara iso
, indicando un cambio de fase de -90 ° (ou 90 graos por diante da corrente).O triángulo dereito do diagrama de fases aclara iso non só está en magnitude senón tamén en relación en fase, co vector de tensión terminal (U) Completando o triángulo.
non só está en magnitude senón tamén en relación en fase, co vector de tensión terminal (U) Completando o triángulo.
Figura 13: diagrama de fases de tensión do circuíto da serie RC
Puntos clave na análise dos circuítos RC da serie
Impedancia no circuíto RC de serie, representada como Z, combina resistencia (R) e o efecto reactivo da capacitancia nunha única medida que varía coa frecuencia do sinal.Exprésase matematicamente como  , onde Ω é a frecuencia angular e C é a capacitancia.Aquí, R constitúe a parte real da impedancia e
, onde Ω é a frecuencia angular e C é a capacitancia.Aquí, R constitúe a parte real da impedancia e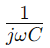 representa a parte imaxinaria, indicando como o condensador inflúe no circuíto.
representa a parte imaxinaria, indicando como o condensador inflúe no circuíto.
 , onde Ω é a frecuencia angular e C é a capacitancia.Aquí, R constitúe a parte real da impedancia e
, onde Ω é a frecuencia angular e C é a capacitancia.Aquí, R constitúe a parte real da impedancia e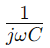 representa a parte imaxinaria, indicando como o condensador inflúe no circuíto.
representa a parte imaxinaria, indicando como o condensador inflúe no circuíto.A forma en que os cambios de impedancia coa frecuencia é fundamental para usar circuítos RC en serie en aplicacións de filtrado.A frecuencias máis baixas, o circuíto presenta unha maior impedancia, bloqueando efectivamente estas frecuencias.Pola contra, a frecuencias máis altas, a impedancia cae, permitindo que estas frecuencias pasen máis libremente.Este comportamento fai que os circuítos RC de serie sexa ideal para tarefas como filtrar ruído de baixa frecuencia non desexado ou pasar sinais de alta frecuencia.

Figura 14: Diagrama de vectores de impedancia do circuíto da serie RC
Conclusión
Desde filtrar as frecuencias non desexadas ata as respostas do sinal de conformación, o circuíto da serie RC é fundamental nunha ampla gama de funcións electrónicas.Ao entender os principios subxacentes como a impedancia, as relacións fasores e o comportamento dependente da frecuencia destes circuítos, enxeñeiros e deseñadores están equipados a solucións artesanais que xestionan efectivamente a integridade do sinal en sistemas electrónicos complexos.O exame detallado destes circuítos, apoiado por análises matemáticas e representacións visuais como diagramas de fases, ofrece unha visión completa que é importante para calquera que busque profundizar na súa comprensión da dinámica de circuítos electrónicos ou para mellorar as súas habilidades prácticas en deseño de circuítos e solución de problemas.
Preguntas frecuentes [preguntas frecuentes]
1. Cal é o principio do circuíto RC?
O principio dun circuíto RC (Resistor-Capacitor) xira arredor dos procesos de carga e descarga do condensador a través da resistencia.Neste circuíto, a capacidade do condensador para almacenar e liberar a enerxía eléctrica interactúa coa resistencia, que controla a velocidade coa que o condensador cobra ou descarga.
2. Por que lidera un circuíto RC?
Nun circuíto RC, a corrente leva a tensión a través do condensador porque o condensador necesita comezar a cargar antes de que a súa tensión poida subir.Dado que a corrente flúe no condensador para cargalo, a corrente pica antes de que a tensión a través do condensador alcance o seu máximo.Este efecto provoca un cambio de fase onde a fase actual leva a fase de tensión ata 90 graos, dependendo da frecuencia do sinal de entrada.
3. Como cambia a tensión nun circuíto RC?
O cambio de tensión nun circuíto RC durante a carga é descrito por unha función exponencial.Cando se aplica unha tensión, a tensión a través do condensador aumenta inicialmente rapidamente, despois diminúe a medida que se achega á tensión de subministración.Matematicamente, isto exprésase como 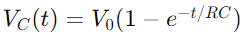 , onde VC(T) é a tensión a través do condensador no tempo t, V0 é a tensión de subministración e RC é a constante de tempo do circuíto, determinando a rapidez co que cobra o condensador.Pola contra, durante a descarga, a tensión a través do condensador diminúe exponencialmente, seguindo a ecuación
, onde VC(T) é a tensión a través do condensador no tempo t, V0 é a tensión de subministración e RC é a constante de tempo do circuíto, determinando a rapidez co que cobra o condensador.Pola contra, durante a descarga, a tensión a través do condensador diminúe exponencialmente, seguindo a ecuación 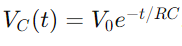 .
.
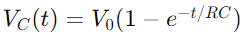 , onde VC(T) é a tensión a través do condensador no tempo t, V0 é a tensión de subministración e RC é a constante de tempo do circuíto, determinando a rapidez co que cobra o condensador.Pola contra, durante a descarga, a tensión a través do condensador diminúe exponencialmente, seguindo a ecuación
, onde VC(T) é a tensión a través do condensador no tempo t, V0 é a tensión de subministración e RC é a constante de tempo do circuíto, determinando a rapidez co que cobra o condensador.Pola contra, durante a descarga, a tensión a través do condensador diminúe exponencialmente, seguindo a ecuación 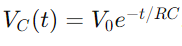 .
. SOBRE NóS
Satisfacción do cliente cada vez.Confianza mutua e intereses comúns.
SOBRE NóS
Satisfacción do cliente cada vez.Confianza mutua e intereses comúns.
proba de función.Os produtos máis rendibles e o mellor servizo son o noso compromiso eterno.
Artigo quente
- Son intercambiables CR2032 e CR2016
- Mosfet: definición, principio de traballo e selección
- Instalación e proba do relevo, interpretación de diagramas de cableado do relé
- CR2016 vs. CR2032 Cal é a diferenza
- NPN vs. PNP: Cal é a diferenza?
- ESP32 VS STM32: Que microcontrolador é mellor para ti?
- LM358 Guía completa do amplificador operativo dobre: pints, diagramas de circuítos, equivalentes, exemplos útiles
- CR2032 VS DL2032 VS CR2025 Guía de comparación
- Comprender as diferenzas Esp32 e ESP32-S3 Análise técnica e de rendemento
- Análise detallada do circuíto da serie RC
 Análise en profundidade de 1N4148 Diodos: modos de funcionamento, especificacións e escenarios de uso
Análise en profundidade de 1N4148 Diodos: modos de funcionamento, especificacións e escenarios de uso
2024-05-08
 Comprender os tipos e usos das bombas de desprazamento dinámicas e positivas
Comprender os tipos e usos das bombas de desprazamento dinámicas e positivas
2024-05-07
Número de parte quente
 C1608X7R1H474M080AC
C1608X7R1H474M080AC C2012X5R1H684K125AB
C2012X5R1H684K125AB CGA9L1X7S3A223M160KA
CGA9L1X7S3A223M160KA CL05B103KA5NNND
CL05B103KA5NNND CC0603ZRY5V6BB684
CC0603ZRY5V6BB684 TAP106K016FAB
TAP106K016FAB 20021321-00016C4LF
20021321-00016C4LF MBRB10100CT
MBRB10100CT IRLS3813TRLPBF
IRLS3813TRLPBF MAX545BCSD
MAX545BCSD
- HIN213ECA-T
- MAX4518ESD+T
- REC5-0505SRW/H4/A
- VI-J30-EW
- VI-220-IX
- 5CGTFD5C5F23I7N
- RT1206DRE0775RL
- MMF400S170U
- FAN5702UMP08X
- AD822BRZ-REEL7
- STM32F103ZDT6
- OPA2336E/250
- LM2852YMXA-1.5
- MC74HC74ADR2G
- AD8315ARMZ-RL
- STR752FR0T6
- 74LV139PW+118
- AM29F040B-70JE/T
- AM29F400BB-90SE/T
- AP7215-33SG
- BA5924FP-E2
- BCM63283KFBG
- CY7C441-20JI
- FXS40IF1-03-A8-QE1-L
- GT8G151LQ
- HC5549CMZ
- IDT74LVCH16374APA8
- LV23002M-TLM-E
- M37560MF-320GP
- MAX8564AEUB
- P89V51RD2FBC557
- QM14N65F
- SST32HF3282-70-4E-LS
- VT233TCX-ADJ-001
- LM3543M-N
- CA251-03
- NCE4688
- MT47H64M16HW-25EH
- RM242-020-241-6400